Evolutionary Optimization: Minimizing the Ackley Function

Introduction

As part of an effort to build an educational toolbox for evolutionary optimization, I developed an Evolutionary Strategy (ES) algorithm to minimize the Ackley function, a well-known multimodal benchmark function used in optimization problems. This project serves as an extension of my study in CISC 455: Evolutionary Optimization, demonstrating key concepts such as adaptive mutation, selection strategies, and fitness evaluation.

This report provides an overview of the implementation, key challenges encountered during development, and improvements made during code review. A video visualization of the optimization process is included to illustrate the trajectory of the algorithm in minimizing the Ackley function.

Purpose

The primary purpose of this project was to create a reusable and modular example of an ES algorithm for educational use in an Evolutionary Optimization class. The code is designed to:

Introduce students to evolutionary algorithms.
Demonstrate the effects of different selection strategies: (μ + λ) and (μ, λ).
Provide insights into the behavior of optimization algorithms on multimodal functions.
Serve as a foundation for extending the implementation to other benchmark functions and problems.

Code Review and Key Improvements

Initial Observations

The initial implementation successfully implemented the Ackley function and basic components of an ES algorithm, including:

Agent Class: Representing individual solutions with position, fitness, and mutation step size.
Population Management: Generating offspring and selecting survivors.
Fitness Evaluation: Accurately computing the Ackley function value for each agent.

However, during testing, it was observed that the algorithm sometimes struggled to converge toward the global minimum. This behavior was traced to limitations in the selection strategy and evaluation count handling.

Key Issues Identified

Selection Strategy Pitfall:
- The initial implementation used a pure (μ, λ) strategy without sufficient offspring (λ) relative to the population size (μ). This led to cases where good solutions from previous generations were discarded entirely, causing the algorithm to lose progress.
- The need for an option to switch between (μ + λ) and (μ, λ) strategies was identified for greater flexibility and robustness.
Eval Count Handling:
- The evaluation count was only updated during offspring generation, excluding the initial population evaluations. This caused confusion about the true computational cost of the algorithm.
Mutation Step Size Tuning:
- The learning rate for step-size adaptation was functional but could lead to overly aggressive changes, causing the algorithm to “jump” out of promising regions of the search space.

Improvements Made

1. Selection Strategy Flexibility

A switch was implemented to allow the user to choose between (μ + λ) and (μ, λ) selection strategies. The select_survivors method was modified to handle both strategies, with safeguards to prevent parameter misuse:

def select_survivors(self, offspring, population_size, selection_strategy):
    if selection_strategy.lower() in ["plus", "+"]:
        combined = self.agents + offspring
        ordered = sorted(combined, key=lambda agent: agent.fitness)
        self.agents = ordered[:population_size]
    elif selection_strategy.lower() in ["comma", ","]:
        if len(offspring) < population_size:
            raise ValueError("For comma selection, the number of offspring must be at least the population size.")
        ordered_offspring = sorted(offspring, key=lambda agent: agent.fitness)
        self.agents = ordered_offspring[:population_size]
    else:
        raise ValueError(f"Unknown selection strategy: {selection_strategy}. Use 'plus' or 'comma'.")

3. Parameter Tuning

The mutation learning rate was fine-tuned to balance exploration and exploitation. The algorithm now adapts step sizes more conservatively, reducing the likelihood of overshooting promising areas.

4. Video Visualization

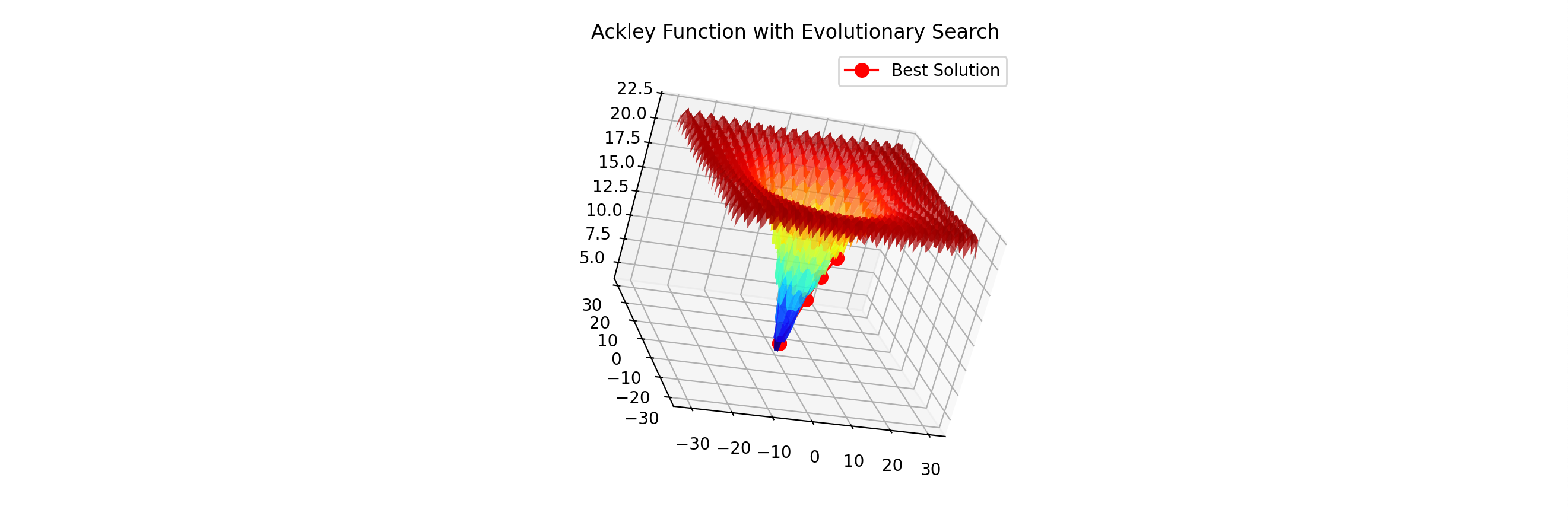
A 3D visualization of the Ackley function and the trajectory of the best solution was implemented using matplotlib. This helps users better understand the algorithm’s progress over generations.

Video Visualization

Below is a video showing the minimization of the Ackley function using the updated Evolutionary Strategy algorithm. The red dot represents the current best solution as it progresses toward the global minimum.

Challenges and Lessons Learned

1. Selection Strategies

The importance of retaining good solutions was reinforced by the observed failure of (μ, λ) selection without sufficient offspring. This highlights the trade-offs between elitism and exploration in evolutionary algorithms.

2. Parameter Sensitivity

Small changes to parameters such as mutation step size and offspring count significantly affected performance. This underscores the need for parameter tuning and robust design.

3. Visualizing Progress

Adding visualization made the optimization process more intuitive, revealing patterns in how the algorithm explores the search space.

Technical Implementation

Algorithm Components

Agent Class: Represents individual solutions with attributes for position, fitness, and mutation step size.
Population Management: Handles offspring generation, mutation, and survivor selection.
Fitness Evaluation: Computes the Ackley function value for each solution.

Key Parameters

Population Size (μ): Number of agents in the population (e.g., 10).
Offspring Count (λ): Number of offspring generated per generation (e.g., 20).
Mutation Step Size (σ): Controls the magnitude of changes to agent positions.
Selection Strategy: Switch between (μ + λ) and (μ, λ).

Results and Impact

The final implementation demonstrated successful minimization of the Ackley function in a neat visualization, converging to a fitness value near 0. Key takeaways include:

Versatility: The code serves as a modular example for extending to other optimization problems. I Intentionally wrote it in an object-oriented format to make it more biologically-inspired.
Educational Value: Clear implementation and visualization will help me to adapt it to new problems.
Robustness: The inclusion of selection strategy flexibility and safeguards ensures better performance and usability.

Conclusion

This project provided a hands-on opportunity to explore evolutionary algorithms and their application to multimodal optimization problems. By addressing challenges such as selection strategy pitfalls and parameter tuning, the final implementation is both educational and practical. It serves as a reusable toolbox component for further experimentation in evolutionary optimization.